Solving an Implicit Relationship with a Newton Solver¶
This tutorial will show how to use a solver to drive some unknown in your model to zero by varying a param. In OpenMDAO you do this by adding a component with an implicit equation, and specifying a nonlinear solver in the containing group.
We will illustrate this with a simple problem.
Find the Intersection of a Parabola and a Line¶
Consider a parabola defined by “y = 3x^2 - 5” and a line defined by “y = -2x + 4”. We would like to find their intersection.
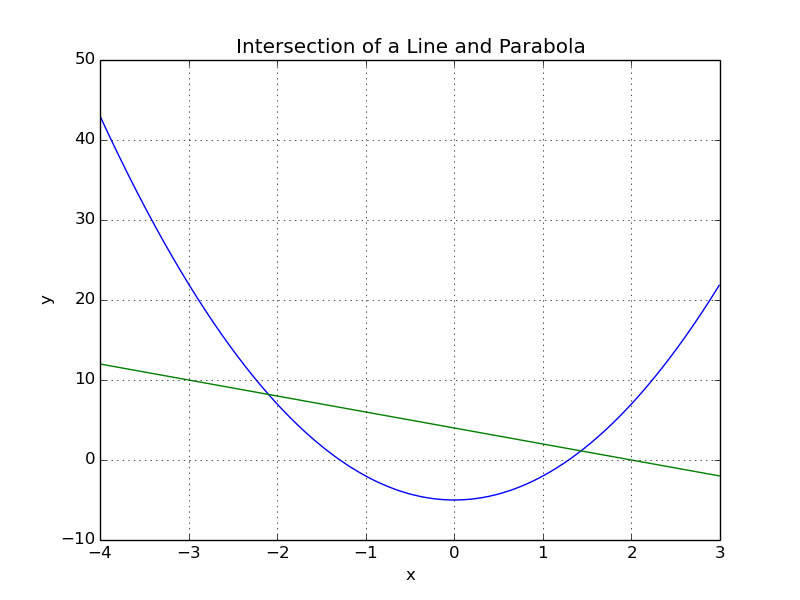
Thie figure above shows that there are two solutions to this problem. We will implement this in OpenMDAO and find both solutions.
For our approach, we will consider the line and parabola as separate disciplines, each requiring its own Component definition that takes a value ‘x’ as an input param, and produces the output ‘y’. Implementing these 2 components with derivatives is straightforward:
from __future__ import print_function
from openmdao.api import Component, Group, Problem, Newton, ScipyGMRES
class Line(Component):
"""Evaluates y = -2x + 4."""
def __init__(self):
super(Line, self).__init__()
self.add_param('x', 1.0)
self.add_output('y', 0.0)
# User can change these.
self.slope = -2.0
self.intercept = 4.0
def solve_nonlinear(self, params, unknowns, resids):
""" y = -2x + 4 """
x = params['x']
m = self.slope
b = self.intercept
unknowns['y'] = m*x + b
def linearize(self, params, unknowns, resids):
""" Jacobian for our line."""
m = self.slope
J = {}
J['y', 'x'] = m
return J
class Parabola(Component):
"""Evaluates y = 3x^2 - 5"""
def __init__(self):
super(Parabola, self).__init__()
self.add_param('x', 1.0)
self.add_output('y', 0.0)
# User can change these.
self.a = 3.0
self.b = 0.0
self.c = -5.0
def solve_nonlinear(self, params, unknowns, resids):
""" y = 3x^2 - 5 """
x = params['x']
a = self.a
b = self.b
c = self.c
unknowns['y'] = a*x**2 + b*x + c
def linearize(self, params, unknowns, resids):
""" Jacobian for our parabola."""
x = params['x']
a = self.a
b = self.b
J = {}
J['y', 'x'] = 2.0*a*x + b
return J
We have made these components slightly more general so that you can, for example, change the slope and intercept of the Line to try solving different problems.
Now we need to add a component that defines a residual for the difference between “parabola.y” and “line.y”. We want to let an OpenMDAO solver drive this difference to zero.
class Balance(Component):
"""Evaluates the residual y1-y2"""
def __init__(self):
super(Balance, self).__init__()
self.add_param('y1', 0.0)
self.add_param('y2', 0.0)
self.add_state('x', 5.0)
def solve_nonlinear(self, params, unknowns, resids):
"""This component does no calculation on its own. It mainly holds the
initial value of the state. An OpenMDAO solver outside of this
component varies it to drive the residual to zero."""
pass
def apply_nonlinear(self, params, unknowns, resids):
""" Report the residual y1-y2 """
y1 = params['y1']
y2 = params['y2']
resids['x'] = y1 - y2
def linearize(self, params, unknowns, resids):
""" Jacobian for our parabola."""
J = {}
J['x', 'y1'] = 1.0
J['x', 'y2'] = -1.0
return J
This component holds both our state and the residual. This component produces no explicit outputs, so the solve_nonlinear method doesn’t do anything (but it still must be declared). In the apply_nonlinear method, we take the difference “y1-y2” and place it in the residual for “x”. The derivatives are straightforward.
Note that the residual equation is not a direct function of the state, but it is indirectly a function via y1 and y2. The partial derivative of the residual with respect to ‘x’ is zero, though the total derivative calculated by OpenMDAO of the residual with respect to ‘x’ is nonzero.
Finally, lets set up the model.
top = Problem()
root = top.root = Group()
root.add('line', Line())
root.add('parabola', Parabola())
root.add('bal', Balance())
root.connect('line.y', 'bal.y1')
root.connect('parabola.y', 'bal.y2')
root.connect('bal.x', 'line.x')
root.connect('bal.x', 'parabola.x')
root.nl_solver = Newton()
root.ln_solver = ScipyGMRES()
top.setup()
Here we connect the output of the Line and Parabola component to the params of the Balance component. The state on “Balance” feeds the params on both components.
To solve this system, we need to specify a nonlinear solver in “root.nl_solver”. There are two types of solvers in OpenMDAO: nonlinear solvers and linear solvers.
A nonlinear solver is used to drive residuals to zero by varying other quantities in your model. The quantities that are varied by the nonlinear solver include all states, but also include any cyclic params on the first component in a cycle. Every unknown in OpenMDAO has a corresponding residual and the nonlinear solver seeks to drive the norm of all the residuals to zero.
A linear solver solves the linearized system of equations in order to calculate a gradient (though there are some other uses too such as preconditioning.)
Every Group contains a linear solver in ln_solver and a nonlinear solver in nl_solver’. The default nonliinear solver is called RunOnce which just runs the components in the group one time without driving the residuals to zero. The default linear solver is LinearGaussSeidel, which is an adequate chain rule solution for the gradient, but must be replaced if your model has cycles or states.
The Newton solver is well-suited for solving this sort of problem, and is the solver you will generally use when solving any system with an implicit state, so we specify Newton in “root.nl_solver”. The Newton solver requires gradients and calculates them through use of the linear solver in “root.ln_solver”. The default solver is LinearGaussSeidel, but to calculate the gradients across a system with implicit states, we should use the ScipyGMRES linear solver, which handles the coupled problem by solving a system of linear equations.
top.run()
print('Solution x=%.2f, line.y=%.2f, parabola.y=%.2f' % (top['bal.x'], top['line.y'], top['parabola.y']))
Running our code should give us an answer:
Solution x=1.43, line.y=1.14, parabola.y=1.14
On Initial Values for States¶
Our problem has two solutions, and we have found one of them. Which solution you arrive at is determined by the initial condition you chose, specifically the solution follows the gradient from the initial point to the solution.
We can find both solutions then:
# Positive solution
top['bal.x'] = 7.0
root.list_states()
top.run()
print('Positive Solution x=%.2f, line.y=%.2f, parabola.y=%.2f' % (top['bal.x'], top['line.y'], top['parabola.y']))
# Negative solution
top['bal.x'] = -7.0
root.list_states()
top.run()
print('Negative Solution x=%.2f, line.y=%.2f, parabola.y=%.2f' % (top['bal.x'], top['line.y'], top['parabola.y']))
OpenMDAO provides a function list_states that lists all the states contained in a group and all of its subgroups. This can be useful in larger nested models that have many implicit components. Since your initial state potentially feeds the initial params in other components, it is important to inspect them to make sure they are correct.
States in model:
bal.x: 7.000000
Positive Solution x=1.43, line.y=1.14, parabola.y=1.14
States in model:
bal.x: -7.000000
Negative Solution x=-2.10, line.y=8.19, parabola.y=8.19
.. tags:: Tutorials
