Hohmann Transfer Tutorial - Optimizing a Spacecraft Manuever¶
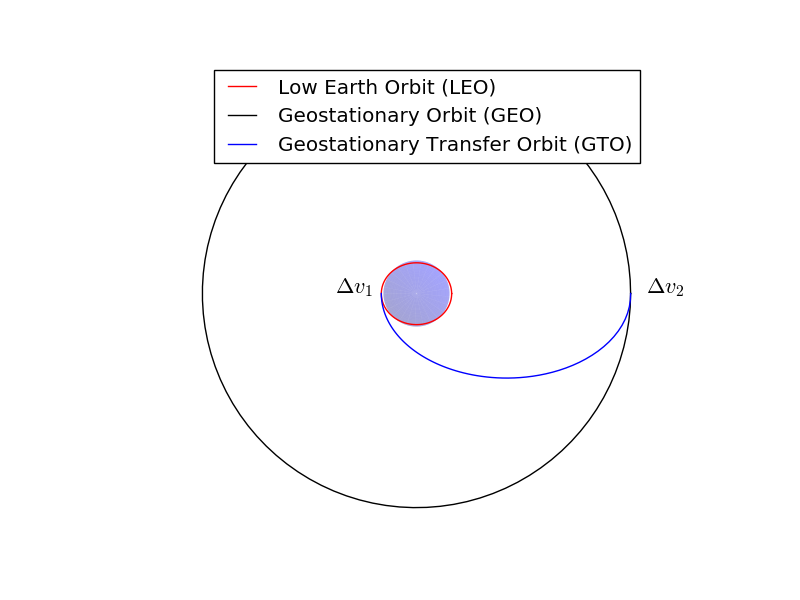
This tutorial will demonstrate the use of OpenMDAO for optimizing a simple orbital mechanics problem. We seek the minimum possible delta-V to transfer a spacecraft from Low Earth Orbit (LEO) to geostationary orbit (GEO) using a two-impulse Hohmann Transfer.
The Hohmann Transfer is a maneuver which minimize the delta-V for transfering a spacecraft from one circular orbit to another. Hohmann transfer’s have a practical application in that they can be used to transfer satellites from LEO parking orbits to geostationary orbit.
To do so, the vehicle first imparts a delta-V along the velocity vector while in LEO. This boosts apogee radius to the radius of the geostationary orbit (42164 km). In this model we will model this delta-V as an impulsive maneuver which changes the spacecraft’s velocity instantaneously.
We will assume that the first impulse is performed at the ascending node in LEO. Thus perigee of the transfer orbit is coincident with the ascending node of the transfer orbit. Apogee of the transfer orbit is thus coincident with the descending node, where we will perform the second impulse.
After the first impulse, the spacecraft coasts to apogee. Once there it impulse a second burn along the velocity vector to raise perigee radius to the radius of GEO, thus circularizing the orbit.
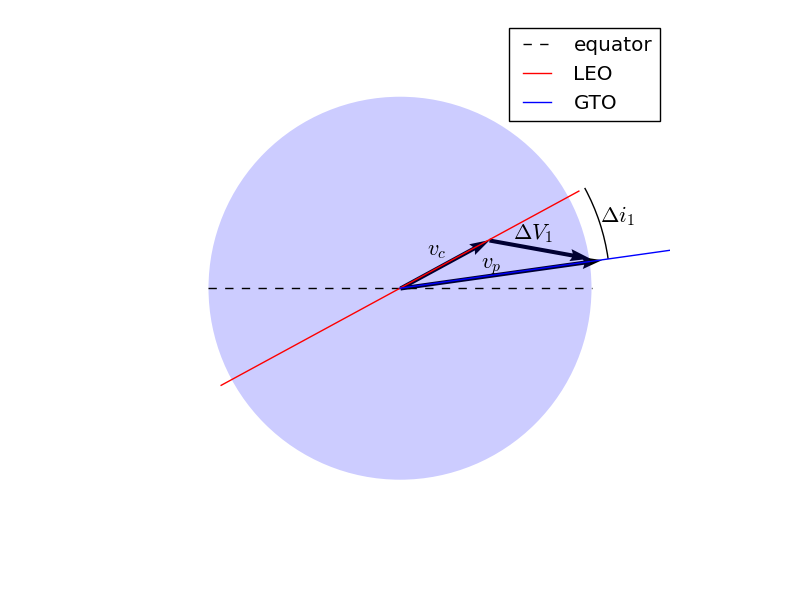
Simple, right? The issue is that, unless they launch from the equator, launch vehicles do not put satellites in a low Earth parking orbit with the same inclination as geostationary orbit. For instance, a due east launch from Kennedy Space Center will result in a parking orbit with an inclination of 28.5 degrees. We therefore need to change the inclination of our satellite during it’s two impulsive burn maneuvers. The question is, what change in inclination at each burn will result in the minimum possible :math:`Delta V`?
The trajectory optimization problem can thus be stated as:
The total \(\Delta V\) is the sum of the two impulsive \(\Delta Vs\).
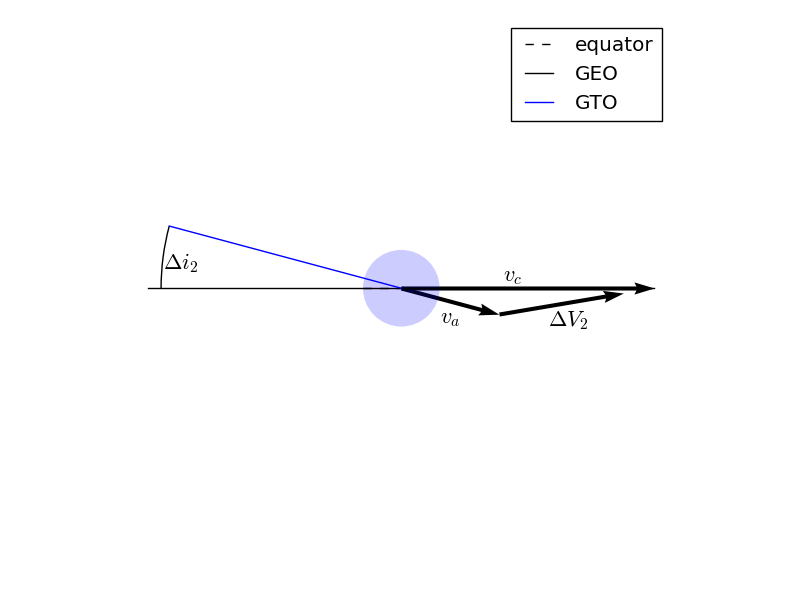
The component of the \(\Delta V\) in the orbital plane is along the local horizontal plane. The orbit-normal component is in the direction of the desired inclination change. Knowing the velocity magnitude before (\(v_c\)) and after (\(v_p\)) the impulse, and the change in inclination due to the impulse (\(\Delta i\)), the \(\Delta V\) is then computed from the law of cosines:
In the first impulse, \(v_1\) is the circular velocity in LEO. In this case \(v_c\) refers to the circular velocity in geostationary orbit, and \(v_a\) is the velocity at apogee of the transfer orbit.
We can compute the circular velocity in either orbit from the following equation:
where \(\mu\) is the gravitational parameter of the Earth and \(r\) is the distance from the center of the Earth.
The velocity after the first impulse is the periapsis velocity of the transfer orbit. This can be solved for based on what we know about the orbit.
The specific angular momentum of the transfer orbit is constant. At periapsis, it is simply the product of the velocity and radius. Therefore, rearranging we have:
The specific angular momentum can also be computed as:
Where \(p\) is the semilatus rectum of the orbit and \(\mu\) is the gravitational paramter of the central body.
The semilatus rectum is computed as:
Where \(a\) and \(e\) are the semi-major axis and eccentricity of the transfer orbit, respectively. Since we know \(r_a\) and \(r_p\) of the transfer orbit, it’s semimajor axis is simply:
The eccentricity is known by the relationship of \(a\) and \(e\) to \(r_p\) (or \(r_a\)):
Thus we can compute periapsis velocity based on the periapsis and apoapsis radii of the transfer orbit, and the gravitational parameter of the central body.
For the second impulse, the final velocity is the circular velocity of the final orbit, which can be computed in the same way as the circular velocity of the initial orbit. The initial velocity at the second impulse is the apoapsis velocity of the transfer orbit, which is:
Having already computed the specific angular momentum of the transfer orbit, this is easily computed.
Finally we have the necessary calculations to compute the \(\Delta V\) of the Hohmann transfer with a plane change.
Components¶
VCircComp¶
VCircComp calculates the circular orbit velocity given an orbital radius and gravitational parameter.
class VCircComp(Component):
""" Computes the circular orbit velocity given a radius and gravitational
parameter.
"""
def __init__(self, radius=6378.14+400, mu=398600.4418):
super(VCircComp, self).__init__()
# Derivative specification
self.deriv_options['type'] = 'user'
self.deriv_options['check_type'] = 'cs'
self.deriv_options['check_step_size'] = 1.0e-16
self.add_param('r',
val=radius,
desc='Radius from central body',
units='km')
self.add_param('mu',
val=mu,
desc='Gravitational parameter of central body',
units='km**3/s**2')
self.add_output('vcirc',
val=1.0,
desc='Circular orbit velocity at given radius '
'and gravitational parameter',
units='km/s')
def solve_nonlinear(self, params, unknowns, resids):
r = params['r']
mu = params['mu']
unknowns['vcirc'] = np.sqrt(mu/r)
def linearize(self, params, unknowns, resids):
r = params['r']
mu = params['mu']
vcirc = unknowns['vcirc']
J = {}
J['vcirc', 'mu'] = 0.5/(r*vcirc)
J['vcirc', 'r'] = -0.5*mu/(vcirc*r**2)
return J
TransferOrbitComp¶
class TransferOrbitComp(Component):
def __init__(self):
super(TransferOrbitComp, self).__init__()
# Derivative specification
self.deriv_options['type'] = 'fd'
self.add_param('mu',
val=398600.4418,
desc='Gravitational parameter of central body',
units='km**3/s**2')
self.add_param('rp', val=7000.0, desc='periapsis radius', units='km')
self.add_param('ra', val=42164.0, desc='apoapsis radius', units='km')
self.add_output('vp', val=0.0, desc='periapsis velocity', units='km/s')
self.add_output('va', val=0.0, desc='apoapsis velocity', units='km/s')
def solve_nonlinear(self, params, unknowns, resids):
mu = params['mu']
rp = params['rp']
ra = params['ra']
a = (ra+rp)/2.0
e = (a-rp)/a
p = a*(1.0-e**2)
h = np.sqrt(mu*p)
unknowns['vp'] = h/rp
unknowns['va'] = h/ra
DeltaVComp¶
class DeltaVComp(Component):
def __init__(self):
super(DeltaVComp, self).__init__()
# Derivative specification
self.deriv_options['type'] = 'user'
self.add_param('v1', val=1.0, desc='Initial velocity', units='km/s')
self.add_param('v2', val=1.0, desc='Final velocity', units='km/s')
self.add_param('dinc', val=1.0, desc='Plane change', units='rad')
# Note: We're going to use trigonometric functions on dinc. The
# automatic unit conversion in OpenMDAO comes in handy here.
self.add_output('delta_v', val=0.0, desc='Delta-V', units='km/s')
def solve_nonlinear(self, params, unknowns, resids):
v1 = params['v1']
v2 = params['v2']
dinc = params['dinc']
unknowns['delta_v'] = v1**2 + v2**2 - 2*v1*v2*np.cos(dinc)
def linearize(self, params, unknowns, resids):
v1 = params['v1']
v2 = params['v2']
dinc = params['dinc']
J = {}
J['delta_v','v1'] = 2*v1 - 2*v2*np.cos(dinc)
J['delta_v','v2'] = 2*v2 - 2*v1*np.cos(dinc)
J['delta_v','dinc'] = 2*v1*v2*np.sin(dinc)
return J
Assembling the Problem¶
prob = Problem(root=Group())
root = prob.root
root.add('mu_comp', IndepVarComp('mu', val=0.0, units='km**3/s**2'),
promotes=['mu'])
root.add('r1_comp', IndepVarComp('r1', val=0.0, units='km'),
promotes=['r1'])
root.add('r2_comp', IndepVarComp('r2', val=0.0, units='km'),
promotes=['r2'])
root.add('dinc1_comp', IndepVarComp('dinc1', val=0.0, units='deg'),
promotes=['dinc1'])
root.add('dinc2_comp', IndepVarComp('dinc2', val=0.0, units='deg'),
promotes=['dinc2'])
root.add('leo', system=VCircComp())
root.add('geo', system=VCircComp())
root.add('transfer', system=TransferOrbitComp())
root.connect('r1', ['leo.r', 'transfer.rp'])
root.connect('r2', ['geo.r', 'transfer.ra'])
root.connect('mu', ['leo.mu', 'geo.mu', 'transfer.mu'])
root.add('dv1', system=DeltaVComp())
root.connect('leo.vcirc', 'dv1.v1')
root.connect('transfer.vp', 'dv1.v2')
root.connect('dinc1', 'dv1.dinc')
root.add('dv2', system=DeltaVComp())
root.connect('transfer.va', 'dv2.v1')
root.connect('geo.vcirc', 'dv2.v2')
root.connect('dinc2', 'dv2.dinc')
root.add('dv_total', system=ExecComp('delta_v=dv1+dv2',
units={'delta_v': 'km/s',
'dv1': 'km/s',
'dv2': 'km/s'}),
promotes=['delta_v'])
root.connect('dv1.delta_v', 'dv_total.dv1')
root.connect('dv2.delta_v', 'dv_total.dv2')
root.add('dinc_total', system=ExecComp('dinc=dinc1+dinc2',
units={'dinc': 'deg',
'dinc1': 'deg',
'dinc2': 'deg'}),
promotes=['dinc'])
root.connect('dinc1', 'dinc_total.dinc1')
root.connect('dinc2', 'dinc_total.dinc2')
prob.driver = ScipyOptimizer()
prob.driver.add_desvar('dinc1', lower=0, upper=28.5)
prob.driver.add_desvar('dinc2', lower=0, upper=28.5)
prob.driver.add_constraint('dinc', lower=28.5, upper=28.5, scaler=1.0)
prob.driver.add_objective('delta_v', scaler=1.0)
# Setup the problem
prob.setup()
# Set initial values
prob['mu'] = 398600.4418
prob['r1'] = 6778.137
prob['r2'] = 42164.0
prob['dinc1'] = 0.0
prob['dinc2'] = 28.5
# Use run_once to evaluate the model at the initial guess.
# This will give us the :math:`\Delta V` for performing
# the entire plane change at apogee.
prob.run_once()
dv_all_apogee = prob['delta_v']
# Go!
prob.run()
print('Impulse 1:')
print(' Delta-V: {0:6.4f} km/s'.format(prob['dv1.delta_v']))
print(' Inclination Change: {0:6.4f} deg'.format(prob['dinc1']))
print('Impulse 2:')
print(' Delta-V: {0:6.4f} km/s'.format(prob['dv2.delta_v']))
print(' Inclination Change: {0:6.4f} deg'.format(prob['dinc2']))
print('Total Delta-V: {0:6.4f} km/s'.format(prob['delta_v']))
print('Total Plane Change: {0:6.4f} deg'.format(prob['dinc']))
print('\nPerforming the plane change at apogee gives a '
'Delta-V of {0:6.4f} km/s'.format(dv_all_apogee))
The resulting output is
Impulse 1:
Delta-V: 5.8132 km/s
Inclination Change: 1.6673 deg
Impulse 2:
Delta-V: 3.1928 km/s
Inclination Change: 26.8327 deg
Total Delta-V: 9.0060 km/s
Total Plane Change: 28.5000 deg
Performing the plane change at apogee gives a Delta-V of 9.0751 km/s
In general, changes in inclination are most efficiently performed at apogee, and on the line of nodes. However, in this case, we see that if we naively perform the entirety of the plane change at apogee, we pay a \(\Delta V\) penalty of about 70 m/s.